Clausal normal form

The clausal normal form (or clause normal form, conjunctive normal form, CNF) of a logical formula is used in logic programming and many theorem proving systems. A formula in clause normal form is a set of clauses, interpreted as a conjunction. A clause is an implicitly universally quantified set of literals, interpreted as a disjunction.^[1]

Conversion to clausal normal form

The procedure to convert a formula into clausal form can destroy the structure of the formula, and naive translations often causes exponential blowup in the size of the resulting formula.

The procedure begins with any formula of classical first-order logic:

Put the formula into negation normal form.
Standardize variables
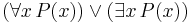- $(\forall x\, P(x)) \vee (\exists x\, P(x))$ becomes 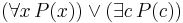$(\forall x\, P(x)) \vee (\exists c\, P(c))$ , where $c$ is new
Skolemize -- replace existential variables with Skolem constants or Skolem functions of universal variables, from the outside inward. Make the following replacements:
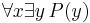- $\forall x \exists y \, P(y)$ becomes 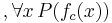$, \forall x \, P(f_c(x))$ , where 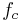$f_c$ is new
Discard the universal quantifiers (which are implicit in CNF).
Put the formula into conjunctive normal form.
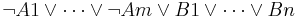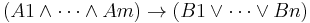Replace $C1 \wedge \cdots \wedge Cn$ with $\{ C1 , \dots , Cn \}$ . Each conjunct is of the form $\neg A1 \vee \cdots \vee \neg Am \vee B1 \vee \cdots \vee Bn$ , which is equivalent to $( A1 \wedge \cdots \wedge Am ) \to ( B1 \vee \cdots \vee Bn )$ .
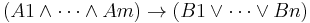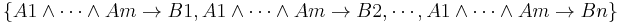Finally, replace each conjunct $( A1 \wedge \cdots \wedge Am ) \to ( B1 \vee \cdots \vee Bn )$ with $\{ A1 \wedge \cdots \wedge Am \to B1 , A1 \wedge \cdots \wedge Am \to B2 , \cdots , A1 \wedge \cdots \wedge Am \to Bn \}$ .

When n ≤ 1 for all clauses, the logic is called Horn clause logic and is equivalent in computational power to a universal Turing machine. Horn logic is the basis of Prolog, the most widely used logic programming language.

Often it is sufficient to generate an equisatisfiable (not an equivalent) CNF for a formula. In this case, the worst-case exponential blow-up can be avoided by introducing definitions and using them to rename parts of the formula. ^[2]

References

^ Loveland, Donald W. (1978). Automated Theorem Proving: A Logical Basis. North Holland.
^ Nonnengart, Andreas; Christoph Weidenbach (2001). "Computing Small Clause Normal Forms". In A. Robinson and A. Voronkov. Handbook of Automated Reasoning. I. Elsevier Science and MIT Press. pp. 335–367. http://www.mpi-inf.mpg.de/~weidenb/publications/handbook99small.ps.gz. Retrieved 2009-07-05.